理解统计相关性的kappa系数
Apr 28, 2017 00:00 · 795 words · 2 minute read
最近尝试对眼底图像进行多分类识别,使用的数据集来自kaggle的Diabetic Retinopathy Detection 。根据眼底图像的好坏分为0,1,2,3,4五类,kaggle的评分基于quadratic weighted kappa,将我们预测的labels与医生手动标注的labels进行通过quadratic weighted kappa进行比较。以前没接触过,在这里简单写一下我对kappa系数的一些理解,如有错误欢迎指出。
简介
Kappa系数是一种比例,代表着分类与完全随机的分类产生错误减少的比例。1960年Cohen等提出用Kappa值作为评价判断的一致性程度的指标,实践证明,它是一个描述诊断的一致性的较为理想的指标,因此在临床试验中得到广泛的应用。 kappa=1 两次判断完全一致 kappa>=0.75 比较满意的一致程度 kappa<0.4 不够理想的一致程度
根据kappa的计算方法分为简单kappa(simple kappa)和加权kappa(weighted kappa),加权kappa又分为linear weighted kappa和quadratic weighted kappa。
linear or quadratic weighted kappa?
关于linear还是quadratic weighted kappa的选择,取决于你的数据集中不同class之间差异的意义。比如对于眼底图像识别的数据,class=0为健康,class=4为疾病晚期非常严重,所以对于把class=0预测成4的行为所造成的惩罚应该远远大于把class=0预测成class=1的行为,使用quadratic的话0->4所造成的惩罚就等于16倍的0->1的惩罚。如下图是一个四分类的两个计算方法的比较。
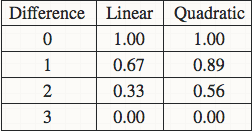
计算方法
Diabetic Retinopathy Detection这里给出了具体计算原理,在python中的实现可参考: https://github.com/benhamner/Metrics/blob/master/Python/ml_metrics/quadratic_weighted_kappa.py
def quadratic_weighted_kappa(rater_a, rater_b, min_rating=None, max_rating=None):
rater_a = np.array(rater_a, dtype=int)
rater_b = np.array(rater_b, dtype=int)
assert(len(rater_a) == len(rater_b))
if min_rating is None:
min_rating = min(min(rater_a), min(rater_b))
if max_rating is None:
max_rating = max(max(rater_a), max(rater_b))
conf_mat = confusion_matrix(rater_a, rater_b,
min_rating, max_rating)
num_ratings = len(conf_mat)
num_scored_items = float(len(rater_a))
hist_rater_a = histogram(rater_a, min_rating, max_rating)
hist_rater_b = histogram(rater_b, min_rating, max_rating)
numerator = 0.0
denominator = 0.0
for i in range(num_ratings):
for j in range(num_ratings):
expected_count = (hist_rater_a[i] * hist_rater_b[j]
/ num_scored_items)
d = pow(i - j, 2.0) / pow(num_ratings - 1, 2.0)
numerator += d * conf_mat[i][j] / num_scored_items
denominator += d * expected_count / num_scored_items
return 1.0 - numerator / denominator